The Silver Lining
My attempt to calculate the central hinge point in this scissor-like shape:
Ratios as measurement or percentage:
64.28… / 35.71…= 1.8
97.40… / 75.76…= 1.28571428…
75.76… - 21.64… / 21.64…= 2.5
75.76… / 21.64…= 3.5
97.40… / 21.64…= 4.5
Set side by side and facing straight on. Left a 2-d square and on the right a cube.
By tilting them 1.485° forward, the back of the cube lifts up matching the 2-d drawing.
360 : 1.485 = 242.4242...(8000 : 33)
A simple construction including the blue infinity line.
It occurred to me that perhaps our physical reality is like a projection unto a screen as
represented by the 2-d drawing. A reflection of the true reality which cannot be
reached physically, as represented by the 3-d or cube drawing. So, no matter where we
are physically, whether in space or earths’ surface, we always exist on a 2-d plane.
Perhaps this is where the flat versus round earth idea originated.
Left and right side enlarged in a straight on view.
Left and right side tilted, exactly matching the π⁴ line, suggesting a precision surveying or
calibration devise. Although interesting there is no way to calculate the central hinge point
exactly, and I changed tactic.
Self explanatory as to how I did this and included are the pyramid lines. In this square all
of the measurements between either vertical or horizontal grid points can be reduced to
numbers without decimal point.
At some point I realized that in order to move forward it requires opposite squares. Everything
has an opposite. This is where things get interesting, because how to know exactly where the
two grids/nets join? Unless they are joined exactly the measurements between upper and lower
grid points will not reduce to numbers without decimal points. However, match the upper and
lower grids perfectly, and the numbers can be reduced to simple numbers not requiring decimal
points. I have found a beautiful method not included here, to do it. Also, if you look closely you
can see a number of circles within the joined grid squares.
From here on remember the number 21.64... (diagram one). Circled in red and right side of the
center line is the area of focus. Left of center line is its inverse and has the same information.
Starting to zoom in to show measurements that can all be reduced to numbers without
decimal places by multiplying mostly by 9, as well as a few other key numbers such as 63.
Enlarging a bit more to show additional measurements.
Enlarging more and moving to the right. These measurements are to the center line.
Here the idea of tube-like is apparent, where π represents the inner lining of a tube.
Imagine looking at an opaque tube which is cut perfectly in half, straight-on from the side.
The inside is not visible but angle it slightly and the inside lining is now visible.
Naturally, all measurements in these drawings are known except the π lines, which
were added because we know what π is and can be used to reverse engineer this design.
Equalizing the square and circle area's are apparent.
The red circle enlarged.
Enlarged further and imagine the eye of a needle.
Three circles and measurements to the left center line and right main circle edge.
(several diagrams up)
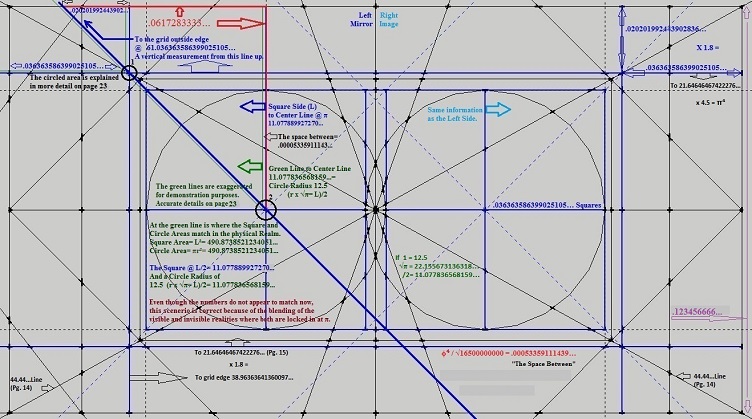
More detail.
Black circled areas 1 and 2 from previous diagram enlarged.
And the attempt at The space between explanation.
See the previous three circles diagram.
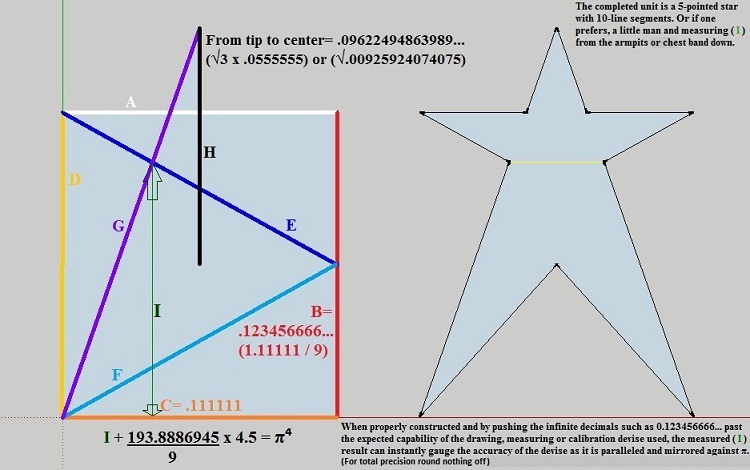
This equation and geometric construction to π is simple and easy to reproduce.
Whether hand drawn on paper, or some other drawing program, or laid out on a level field
as a surveying exercise, this design will reflect its exactness by the number of correct π
decimal places extracted from it.
A fun challenge to see how many π decimal places one can attain. I foresee this diagram
to be used as an educational, hands-on and learning about pi project for children.
Even with a hand drawn diagram using only a pencil and straightedge one can construct π
to an accuracy of about 5 decimal places. The decimal places can be moved depending on the
size of the diagram, but obviously all of the numbers that belong to the diagram must have
their decimal places moved by the same amount. Once the " I " measurement has been
established the decimal must be moved in front of it to complete the equation.
This method based on the constant π can be used as the standard to which the accuracies
of the various measuring, drawing, and calibration programs can be compared. In other words,
measurements can be instantly compared to pi digits because they parallel them.
At the decimal place where pi digits go wrong the measurement is also inaccurate.
For example, the distance of a moving target is instantly gauged against π for accuracy.