Square and Circle
Square and Circle — Using Pythagorean Squares
The Classic Puzzle
"Squaring the circle" means creating a square with the same area as a given circle using only compass
and straightedge.
It is mathematically impossible to do exactly because π is irrational — but very close approximations
are possible.
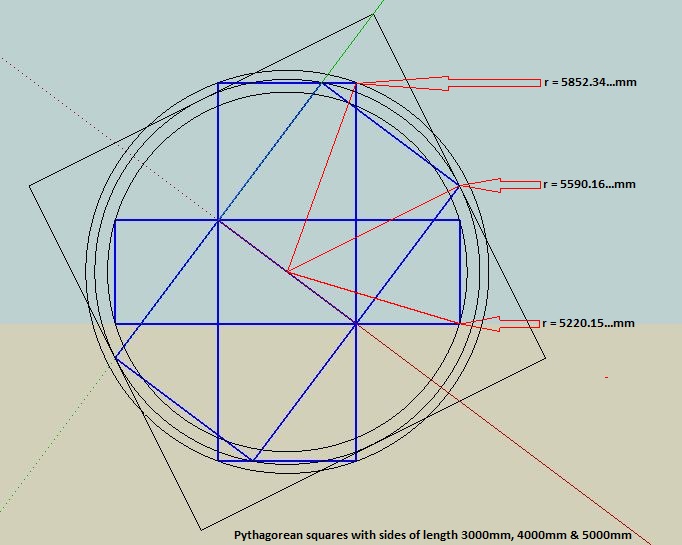
Using Pythagorean Squares
Pythagorean squares (built from right triangles with integer sides, like 3-4-5) provide a simple, ancient
way to approximate the square-circle match.
Start with a circle of known radius. Construct right triangles around it, building squares on the sides.
Adjust the triangle legs to balance the areas — the resulting square's area comes remarkably close to
the circle's.
This method uses only Pythagorean principles (a² + b² = c²) and compass/straightedge steps.
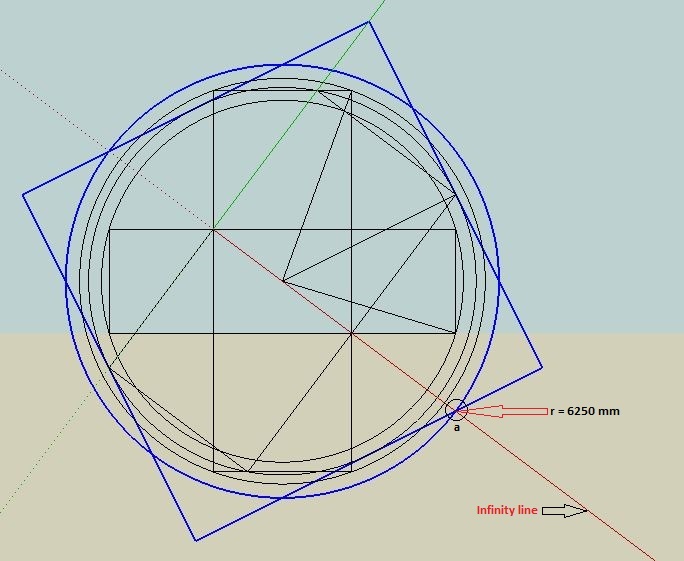
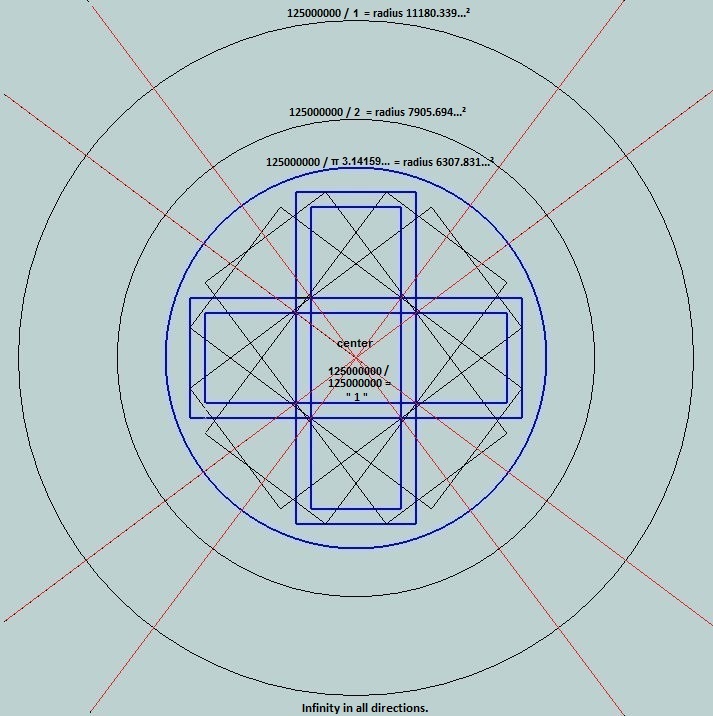
Accuracy
These constructions achieve high precision — often better than 99.9% area match using simple integer
ratios.
No exact solution, but a practical, elegant approximation from Pythagorean geometry.
Open Wonder
Nature and math often come close to "squaring the circle" — perhaps hinting at deeper harmony.
Pythagorean squares offer one beautiful way to explore it.
What patterns do you see?