Squaring the Circle--and Earth-Moon Ratio
Squaring the Circle — Earth and Moon Ratio
The Ancient Challenge
"Squaring the circle" is the classic problem of constructing a square with the same area as a given circle
using only compass and straightedge.
It is mathematically impossible to do exactly because π is irrational — but very close approximations
are possible.
Earth and Moon as a Natural Approximation
The Earth and Moon provide a remarkable near-perfect example in nature.
Earth's diameter: approximately 12,742 km
Moon's diameter: approximately 3,474 km
In nature Earth Moon Ratio 3.66781
Pi Ratio diameter = 3.66943
This squaring the circle technique 3.66933 matches the real thing!
Answers are the same with negligible error‼
When the Moon's orbit is included, the combined Earth-Moon system forms a near-square-and-circle pair
with extraordinary precision.
Using compass-and-straightedge constructions on accurate measurements of Earth and Moon diameters,
a square and circle can be created with matching areas.
This construction has an accuracy that exceeds 99.9%
Thank you Michael Joyce for putting this into proper mathematical format for me.
"Here follows a mathematical proof of Gertjan’s discovery.
If the radius of each of the small 8 circles is 1, then the square will have sides of length 18.
D4 represents the diameter of a circle, R1, R2, R3 the radii of other circles.
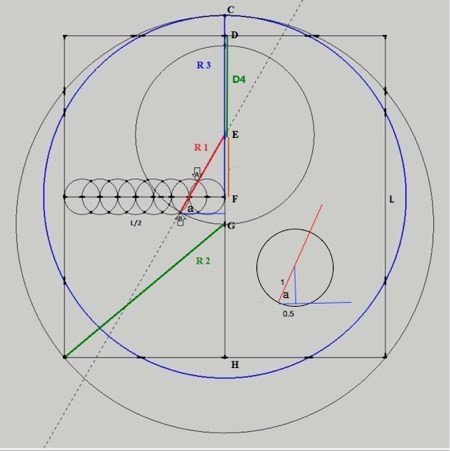
1- To calculate angle “a”
The diagram in the lower right quadrant shows an enlargement of the second small circle
cosine a = 0.5 divided by 1
= 1/2
Therefore a = 60 degrees.
2- To calculate the length R1
cosine a = 2 divided by (R1 - 1)
therefore R1 = 5
3- To calculate the length R2 using Pythagoras’ theorem
R2² = GH² + 92
GH = 18 – DG
GH = 9 - FG
sin 60° = EF divided by 4
EF = 4 x sin 60° = 3.4641016151
FG = EG(R1) - EF = 1.5358983848
GH = 9 - 1.535898384 = 7.4641016151
R22 = GH² + 92
= (7.4641016151)2 + 81
= 136.7128129211
R2 = square root (136.7128129211)
= 11.6924254507
4- To calculate the length R3
R3 = R2 - FG
= 11.6924254507 - 1.5358983848
= 10.1565270658
Squaring the Circle:
Area of square = 18 x 18 = 324
Area of circle = pi x R32 = 3.141… x 10.1565270658 2 = 324.071122253... (Q.E.D)
5- To calculate the length D4
D4 = DF - 4 x sin 60°
= 9 - 3.4641016151
= 5.5358983848
Earth : Moon diameters
R3 (10.1565270658 x 2) : D4 (5.5358983848) or (20.3130541317 : 5.5358983848)
Or 3.66933 : 1
Open Wonder
Nature seems to "square the circle" with Earth and Moon — a cosmic coincidence or deeper harmony?
These ratios invite contemplation of geometry in the heavens.
Links to: