Prime Numbers and Vibrating Strings

Primes are the atoms and basic building blocks of mathematics. The challenge for hundreds of years
has been to decide whether a given number is a prime or not, and to find a pattern in the distribution
of the primes. Shown below is the perfect pattern in the distribution of the primes and non-primes.

Instead of looking for a pattern in the prime numbers, I began looking for it in the non-prime numbers.

I first observed that prime number 3 is followed by repeating segments of 6, which consist solely
of non-prime numbers. (Non-prime numbers blue and green, and prime numbers colored orange)

The lines between the twin prime sets, such as 11/13 and 17/19, show that all of the sections
between them consist of multiples of 3. (these lines suggest spectral rays in the EM spectrum)

When lining up the segments of 6 horizontally, I noticed a zigzag pattern like a frequency wave,
starting with prime number 3. The rest of this "frequency wave" consists of non-prime numbers,
with numbers bouncing from prime #3 to 9 to 15 etc. at regular intervals of 6.
(vertical spacings are added for easier viewing)

The finding of #3-frequency wave, was quickly followed by the #5-frequency pattern.

From here I continued with 20 or so additional sequential frequency waves.
(EM frequencies, vibrating strings, waves, signals, oscillations, etc..?)

Every prime number like a musical note, is followed by a vibrating string. And, like finely
woven threads of fabric, all of these strings are made up entirely of non-prime numbers.
To know the note, you must first hear the sound!
A brilliant quote by Mozart: “The music is not in the notes, but in the silence between‎‎.”

Imagine for a moment prime numbers as stars, and vibrating strings as space.
Interestingly, while we in the west generally look for patterns in the stars,
Australian aboriginals look for patterns in the spaces between the stars.

A few points to remember before going forward:

- The #1 chief frequency wave is comprised of odd numbers, both prime and non-prime numbers.
- Grid lines represent all even numbers, including the number 0.
- And, since number 2 is part of the grid matrix, it is not a true prime number.
- The zero-point like the narrowest point in an hour glass, is indicated by the red pins/pegs.
- Originating from the zero-point, the first number (prime or non-prime) beginning each string,
- is followed exclusively by non-prime numbers.
- The first few strings/frequencies, cover most of the non-prime numbers on the entire #1 strip.

Before continuing, several ideas that may relate to the subject matter as explained in this page:

UFO/UAP/USO/AVCraft must have advanced hull material and properties,
to be able to maneuver and do the things that they appear to do.

The hull/craft materials likely consist of special metals and specific amounts, blended together
on an atomic/isotope level in such a way, that their wave arrangements mirror the #1 frequency,
and all or some of its perfectly interwoven (based on prime numbers) frequency wave arrangements.

Such a craft could do amazing things, such as levitation, where an electromagnetic force can
manipulate the gravitational force in all directions. I have witnessed such an example in 1977,
identical as seen in this video clip. As good luck would have it my sighting was in a clear blue sky.

Spheres (probes) released from discs which in turn belong to huge cigar shaped motherships.
“The only force you need to counter is the electromagnetic force” Nikola Tesla

Continuing:

The numbers belonging to the #3 string as mentioned earlier, occur at intervals of 6.
The #5-string has intervals of 10, number 7 has 14, number 9 has 18, and so on.
It increases by 4 each time. For example 3-9-15…, 5-15-25…, 7-21-35…, 9-27-45… etc.
(when the vertical spacing's for easier viewing are eliminated, the increases are 2)

As the numbers beginning each new vibrating string 1,3,5,7,9, etc., after the zero-point
as represented by the red pins grow larger, their wave segments as shown stretch accordingly.
These segments match each other in specific ways:
For example, five #7 segments = seven #5 segments. Five #11 segments = eleven #5 segments.
Seven #11 segments = eleven #7 segments. Etc. The strings contain many interesting patterns.

If prime number 3 were a musical note with wave segments of 6, then all of the related vibrating
strings beginning with 9,15,21, etc. have increasingly longer segments, or better said, a changed
or slowed down tempo of the musical note, prime number 3.

Next, prime number 5 “musical note”, with its wave segments of 10. Again, the subsequent
vibrating strings or frequencies beginning with 15,25,35, etc. are a changed or slowed down
tempo of the same musical note, prime number 5.
Etc. (In music lingo slowed down notes have proper expressions)

Again, all string numbers following the prime numbers consist of non-prime numbers.

By knowing the shape and arrangements of the frequency waves, one can predict prime numbers a
million miles down the strip. Nevertheless, how to know exactly at which points along the strip new
frequencies are required, is explained with this important discovery, I call it the "pyramid strip".

The Pyramid strip overlays the #1 (C) frequency wave. It determines exactly where,
and how far along the strip, the primes and their string insertion points are located,
depending on the need to know the size of the numbers.

Again, the #3-string covers all other related frequencies such as 9-15-21-27-etc., so that after
the first small pyramid 1-9-25 no other pyramid peaks are required, and only the base line numbers
are used from here on. The spacing ratio for the bottom line is 1²-5²-7²-11²-13²-17²-19²-23²- 25² etc.,
(4-2-4-2-4-2-etc). Alternatively as ratios 2-1-2-1-2-1 or 1-0-1-0-1-0 etc.

However, 25² and all numbers that are part of the prime #5 string sitting on these
ratio points could also be eliminated, but the consistent 4-2-4-2-4 pattern would be lost.
This idea continues with the next string #7 and 49² for example.

These pyramids continue to stretch with predictable increases along a seemingly straight line,
while their heights remain unchanged, 3 squares up and 4 down. However, straight lines do not
exist and it indicates an arc/circle. This circle (perhaps magnetism) loops back to the zero point,
and together with its opposite circle (perhaps electricity) looks like the number 8 or infinity symbol.

To demonstrate how perfect and orderly the prime numbers colored orange, are entangled
like a seed in a fruit, and fit untouched between all of the frequency waves, I made a #1-frequency
board with only the prime numbers marked on it in their proper place. And I made transparent
strips, marked with the correct numbers for each of the following strings that will overlay it.

Begin by placing the #3 string frequency on the #1 board,
which fills in all of the non-prime numbers to 25 (5²).

The #5 string fills in the non-prime numbers to number 49 (7²),
leaving only prime numbers marked as orange.

String #7 to 121 (11²)

String #11 to 169 (13²)

String #13 to 289 (17²)

Place string #17 and continue like this.

It effectively separates and sifts out the prime numbers from the non-prime numbers.
Example: At number 25 (5²) enter string #5, at number 49 (7²) enter string #7, and so on.

Imagine a train moving along a train track and passing known and predetermined stops along
the way. At each stop a new string is engaged to cover all non-prime numbers on the strip
up to the next stop and ahead of the train. As the distances between stops increase continually
the train can speed up since there are fewer stops and strings required. Again, distance and
speed increases but the string numbers decrease. In other words, placing progressively longer
sections of track ahead of a faster and faster moving train.
Compare to the infinity π line and a thought-provoking postulation by David.

The measurements for the stops along the primes-board increase at predictable intervals:
Red = 1”-3”-5”-7”-9”-etc, and green sections 1”-2”-3”-4”-5”-etc. (The strip has 4 squares per inch)
Reminds me of a universe that is expanding at an accelerating rate.

Imagine this primes-board represents a line of sight looking out into the universe from 0 (the peg).
Meaning from any position in space, and where from that position it appears to be expanding same
as the prime numbers, at an increasing but predictable rate. So, logically, an "expanding" universe
already consists of pre-existing ever-growing numbers, vibrating strings, patterns, and primes.

What Riemann observed in his mathematics were the peaks and valleys of waves/strings with
a common line running through them, the zero line. (Image from the The story of Math DVD)

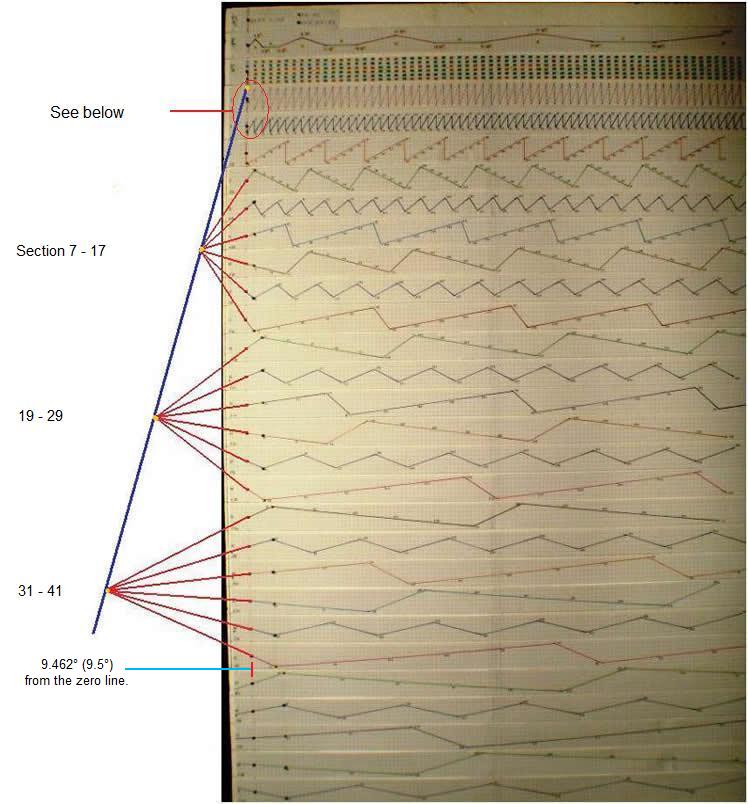
The strings are separated for display purposes, and so the zeros lie in an illusory straight line.

Compare the vertical sections such as section 7 to 17 on the strip below, with the separated
string layouts on the board. Observe how the waves are shaped, and how the 6 string sections
merge to points on the left side of the so-called zero line.

Those points west of the zero line show-increasing intervals of 3”. E.g., strings 11 and 13 merge at 3”
west of the zero line and strings 23 and 25 merge 6” west of the zero line. Connecting those points
on the left side of the zero line will produce a line intersecting with the zero line at -6, and
tapering away from the zero line at 18.4°. The triangle consists of angles 90°, 71.6°, and 18.4°.
Again, to this point the vertical spacing's were added for easier viewing!

The #1-Frequency correctly displayed without vertical spacing's. (triangle = 90°, 80.5°, 9.5°)

From the strip board peg (zero point, infinity, the source, singularity?, etc.), and this example
of six strings (section 7 to 17), show that all of them emanate from a single source reversal point!
Therefore, section 7 to 17 as the start of those 6 strings, and section -17 to -7 mirroring those
vibrating strings, occur simultaneously. (The zero-point represents the infinity symbol center)

Ideas:
Simultaneous opposing positions between entangled quantum particles, i.e. particles of light?
Prime numbers as entangled particles, and intersecting vibrating strings smaller sub particles?

In flat 2-d form all frequencies emanate from a single source zero point, but due to twisting the flat
2-d into the correct 3-d form, it shows that in tubular 3-d form there appear to be two zero points.
However, the real point of origin is the center of the tube. The point of Origin or infinity point is
the source of all spiraling frequencies, like the center of a pie cut in 6 even slices!
It is the midpoint between positive and negative numbers, the midpoint of image reversal in a lens,
or the point between two realities.

The distance the six string/waves (7 to 17) are from the Origin before they line up vertically
like they did at the start even though they are now inverted, is 382882.5 mm x 2= 765765 mm.
(Squares are 1 mm)

(The LCM is 7 x 9 x 11 x 13 x 15 x 17= 2297295 / 6= 382882.5)
1 section - 11 x 13= 143 mm-----------x 53550 = 765765 (143 mm from point of Origin)
9 sections - 9 x 15= 135 mm-- 15 mm x 51051 = 765765 ( 15 mm from point of Origin)
1 section  - 7 x 17= 119 mm------------x 64350 = 765765 (119 mm from point of Origin)

Like increasing ripples in a circular pond for the subsequent wave sections such as 19-29, 31-41 etc.

Frequencies accurately shown as tubular, circular and spiralling, instead of flat and straight.
And as conjectured earlier, the #1 ultra high frequency wave as represented by the tube
contains the entire EMF spectrum.
All frequencies coming out of a tiny zero point in such an perfect and organized manner???

Imagine this tube as the barrel of a gun, and the spiralling pattern of frequency 3, as the rifling.
So, the further down the barrel, away from the zero point you go, the larger the numbers and
denser the frequencies become. What are the possibilities here?

In the Netherlands when someone dies, they have an interesting saying, "de pijp uit gaan".
Translated it says, "exiting the tube". Traveling from entry point to exit point and over again?
It seems so according to the mathematical model described here, because the perfect
arrangement of primes, non-primes and frequencies exist in this tubular model as shown.

Frequency #3 appears to have stronger bonds than the others.

A connection to this verse perhaps: "Or ever the silver cord be loosed," Ecclesiastes 12:6 KJV

Prime numbers, orange (3-d) and black (2-d), may represent a melodic language.
Perhaps one day prime numbers will be used in cutting-edge communication methods.

With this discovery and by knowing the string/wave patterns, it is possible to decode encrypted
numbers by finding the primes that created this number. Because without knowing the original
primes it is almost impossible to decode that number. Simply locate the encoded number on the
#1-frequency strip, and observe the prime frequencies attached to it.
For example, the following numbers are the product of two prime numbers:

Product               Primes (frequency numbers)
15           =           3 x 5
77           =           7 x 11
221         =          13 x 17

To sum up, the first nine squares represent all of the prime and non-prime numbers.
The diagonal lines represent the frequencies as they cancel out all of the yellow non-prime
numbers, leaving only the red prime numbers.
Therefore, by knowing exact and predictable frequency patterns, mathematicians should
be able to find a formula to see whether a given number is a prime or not.

Non-prime number frequencies have patterns, therefore prime numbers have inverse patterns.
A shape cut out of a piece of paper always leaves an inverse cut-out pattern.

This next section contains additional ideas:

Prime numbers, the Golden spiral in 3-d, and where the 0 point represents the start and finish:

Looking into the tube or frequencies toward the zero point, is like looking into the
Golden ratio spiral with its excentric or concentric spiral motion.
The #1-frequency represents the entire golden ratio spiral, 1-3-5-7 etc., with each added frequency
forming increasingly complex geometric and fractal like repeating patterns.
The 3-frequency makes ¾ turns 3-9-15 etc. (Example section 9 to 15 in blue.)
The 5-frequency makes 1-1/4 turns, 5-15-25 etc. The 7-frequency makes 1-3/4 turns, 7-21-35 etc.

This next sieve method for finding prime numbers begins with several observations:

The top row of numbers spaced at regular intervals of 6 (3 - 9 - 15 - etc.) represents the
#3-frequency wave's non-prime numbers as identified in my first sieve find.

Imagine the O in the top left corner as the point of Origin or infinity, and the source of light.
The top 1 small square represents the main square (grid paper, universe?) however large it may be.
So when looking towards the point of Origin, or the top left corner of the small square,
it appears that this idea repeats itself going in both directions (multi-verses, extra-dimensional?).

Imagine that the blue lines are light rays passing through the grid paper, which has pinholes
at the center of certain squares for the light to pass through. Again, the horizontal top row of
numbers 3-9-15-21-etc. through which the blue lines pass through first, are numbers belonging to
the #3-frequency wave.

None of the squares representing the orange prime numbers, is ever intersected dead center
by any blue frequency waves, only the non-prime number squares are, and so the prime numbers
(free-spaces) are free to drop out as in a Tetris game, down to the 45°- #3 diagonal line.

The angle between #3 and #9 lines is 26.565°. It is also the passageway angle within the Great Pyramid.

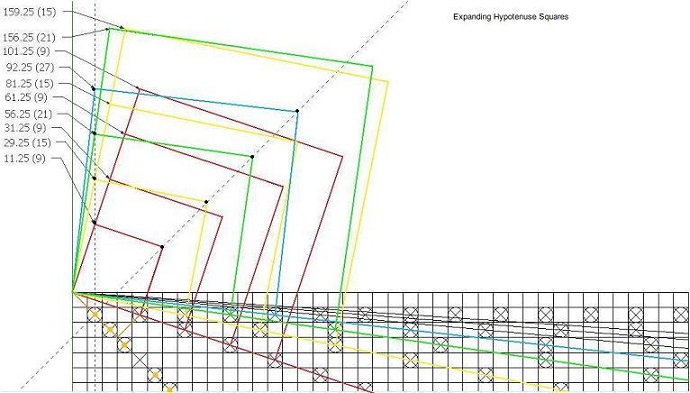
The top corners for each square, representing frequency numbers 9, 15, 21, 27, etc. are evenly spaced
as indicated by the black dots, and as in the diagram all the other squares have similar arrangements.

All expanding right-angled triangles originate from the zero point in the upper left corner.
Shown here are the first few right-angled triangles beginning the primes sieve.
All triangles consist of non-prime numbers.

The first red right triangle 3² + 1.5²= 11.25 (A² + B²= C²), and so on.

The small orange triangle 1² + .5² = 1.25 is distinct from the others, because it resides above
all of the numbers! The 1 small square in the upper left corner is a copy of the entire main square
(grid paper) and so on.

With this basic information showing an indefinite and regular progression of eight, the successive
hypotenuses can be determined without much effort.

The material in this web-page may help to clarify other outstanding areas concerning prime
numbers such as the “Twin prime problem” and the “Goldbach conjecture”.

Return to top